Задача повышенной сложности, часть с

Задания второй части профильного экзамена

В эту часть вошли непростые, комбинированные задачи, однако научиться решать можно каждую.

Задание №13 посвящено уравнениям: тригонометрическим, показательным и другим. Всё чаще в этом номере дают комбинаторное уравнение — логарифм плюс тригонометрия и другие вариации.

В задании №14 вам предлагается решить стереометрическую задачу. Она может быть на объём многогранников и их сечения или нахождение расстояния между прямой и плоскостью. Чтобы решить эти задачи, нужно хорошо знать теорию и много практиковаться. 

В задании №15 вам встретятся неравенства: смешанные, иррациональные или неравенства, содержащие модуль.

Для решения задачи №16 нужны твёрдые знания по планиметрии. Это задание проверяет ваше умение находить элементы трапеции, треугольника, окружности и других фигур. 

Задание №17 часто называют экономикой, так как оно связано с финансовой математикой. Вам может попасться задача о кредитах: например, на поиск суммы платежа, процентной ставки или срока. Также в этом номере вы можете встретить задачу на вклады или оптимизацию. Решение потребует большого количества вычислений, поэтому развивайте навык быстрого счёта.

Одно из самых сложных заданий ЕГЭ по профильной математике 2021 — №18. Это задача с параметром. В школе эту тему часто обходят стороной. Прежде чем приниматься за решение, нужно хорошо повторить функции, их свойства и графики.

Задание №19 — нестандартная задача, можно сказать, олимпиадного уровня. Она проверяет умение строить и исследовать простейшие математические модели. Вам помогут логика и хорошее знание математики в целом.

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Логарифмические уравнения

Логарифмическими уравнениями называют уравнения вида $log_{a}f(x)=log_{a}g(x)$, где $а$ – положительное число, отличное от $1$, и уравнения, сводящиеся к этому виду.

Для решения логарифмических уравнений необходимо знать свойства логарифмов: все свойства логарифмов мы будем рассматривать для $a > 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log_{а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

Пример:

$log_{3}3^{10}=10log_{3}3=10;$

$log_{5^3}7={1}/{3}log_{5}7;$

$log_{3^7}4^5={5}/{7}log_{3}4;$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_a(bc)=log_{a}b+log_{a}c$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b∙log_{c}d=log_{c}b∙log_{a}d$, если $a, b, c$ и $d > 0, a≠1, b≠1.$

5. $c^(log_{a}b)=b^{log_{a}b}$, где $а, b, c > 0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Можно выделить несколько основных видов логарифмических уравнений:

— Простейшие логарифмические уравнения: $log_{a}x=b$. Решение данного вида уравнений следует из определения логарифма, т.е. $x=a^b$ и $х > 0$

Пример:

$log_{2}x=3$

Представим обе части уравнения в виде логарифма по основанию $2$

$log_{2}x=log_{2}2^3$

Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.

$x = 8$

Ответ: $х = 8$

— Уравнения вида: $log_{a}f(x)=log_{a}g(x)$. Т.к. основания одинаковые, то приравниваем подлогарифмические выражения и учитываем ОДЗ:

$\table\{\ f(x)=g(x);\ f(x)>0;\ g(x) > 0, а > 0, а≠1;$

Пример:

$log_{3}(x^2-3x-5)=log_{3}(7-2x)$

Т.к. основания одинаковые, то приравниваем подлогарифмические выражения

$x^2-3x-5=7-2x$

Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые

$x^2-x-12=0$

$x_1=4,x_2= -3$

Проверим найденные корни по условиям $\table\{\ x^2-3x-5>0;\ 7-2x>0;$

При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень

Ответ: $х=-3$

Метод замены переменной.

В данном методе надо:

1. Записать ОДЗ уравнения.
2. По свойствам логарифмов добиться того, чтобы в уравнении получились одинаковые логарифмы.
3. Заменить $log_{a}f(x)$ на любую переменную.
4. Решить уравнение относительно новой переменной.
5. Вернутся в п.3, подставить вместо переменной значение и получить простейшее уравнение вида: $log_{a}x=b$
6. Решить простейшее уравнение.
7. После нахождения корней логарифмического уравнения необходимо поставить их в п.1 и проверить условие ОДЗ.

Пример:

Решите уравнение $log_{2}√x+2log_{√x}2-3=0$

Решение:

1. Запишем ОДЗ уравнения:

$\table\{\ х>0,\text»так как стоит под знаком корня и логарифма»;\ √х≠1→х≠1;$

2. Сделаем логарифмы по основанию $2$, для этого воспользуемся во втором слагаемом правилом перехода к новому основанию:

$log_{2}√x+{2}/{log_{2}√x}-3=0$

3. Далее сделаем замену переменной $log_{2}√x=t$

4. Получим дробно — рациональное уравнение относительно переменной t

$t+{2}/{t}-3=0$

Приведем все слагаемые к общему знаменателю $t$.

${t^2+2-3t}/{t}=0$

Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.

$t^2+2-3t=0$, $t≠0$

5. Решим полученное квадратное уравнение по теореме Виета:

$t^2-3t+2=0$

$t_1=1; t_2=2$

6. Вернемся в п.3, сделаем обратную замену и получим два простых логарифмических уравнения:

$log_{2}√x=1$, $log_{2}√x=2$

Прологарифмируем правые части уравнений

$log_{2}√x=log_{2}2$, $log_{2}√x=log_{2}4$

Приравняем подлогарифмические выражения

$√x=2$, $√x=4$

Чтобы избавиться от корня, возведем обе части уравнения в квадрат

$х_1=4$, $х_2= 16$

7. Подставим корни логарифмического уравнения в п.1 и проверим условие ОДЗ.

$\{\table\ 4 >0; \4≠1;$

Первый корень удовлетворяет ОДЗ.

$\{\table\ 16 >0; \16≠1;$ Второй корень тоже удовлетворяет ОДЗ.

Ответ: $4; 16$

Уравнения вида $log_{a^2}x+log_{a}x+c=0$. Такие уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению. После того, как корни уравнения будут найдены, надо отобрать их с учетом ОДЗ.

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Теория к заданию 4 из ЕГЭ по математике (профильной)

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}{-}$.

$Р(А)+Р{(А)}{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:

$Р(А+В)=Р(А)+Р(В)-Р(А·В)$

В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.

Решение:

Обозначим события, пусть:

$А$ = кофе закончится в первом автомате,

$В$ = кофе закончится во втором автомате.

Тогда,

$A·B =$ кофе закончится в обоих автоматах,

$A + B =$ кофе закончится хотя бы в одном автомате.

По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.

События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:

$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$

Ответ: $0,88$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Прямоугольный треугольник

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. 

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника. (Рис.14)

Один острый угол прямоугольного треугольника на $44°$ больше другого острого угла. Найдите больший острый угол.

Решение:

В прямоугольном треугольнике $АВС$ $∠А$ и $∠В$ – острые.

Пусть $∠ А – х$, тогда $∠ В — (х+44)$.

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

На основании этого правила, составим и решим уравнение:

$х+х+44=90$

$2х+44=90$

$2х=90-44$

$2х=46$

$х=23$

Угол $В$ больший в этом треугольнике, через $«х»$ он записывался как, $х+44$, следовательно, $∠В=23+44=67°$.

Ответ: $67$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$ 

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. Основное тригонометрическое тождество: $sin^2x+cos^2x=1$
6. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
7. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
8. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Какие темы важно знать для ЕГЭ по математике 2022?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул

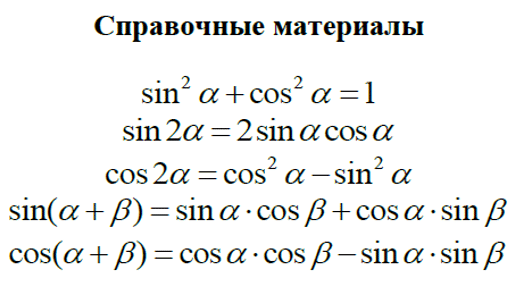
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем

Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

Советы по подготовке к ЕГЭ по профильной математике 2021

Повторите теорию

Не откладывайте на потом. Вспомните все определения, формулы и понятия перед там, как приступать к решению задач. Попробуйте писать формулы по памяти, а потом сверять

И не забывайте: важно не вызубрить темы, а понять их. 

Не пропускайте первую часть

Одна из грубых ошибок — переходить сразу к решению второй части ЕГЭ. Многие задачи из первой решаются довольно просто, но не стоит их недооценивать. Они составлены так, чтобы проверить не только навык решения, но и внимательность к деталям. Прорабатывайте номера из первой части, ведь для достижения цели важен каждый балл. 

Внимательно читайте текст заданий

Смотрите, в каких единицах измерения требуется ответ и нужно ли его округлять

В задании №7 важно понимать, какой график вам дан — производной или функции. От этого зависит ответ на заданный вопрос

В экономической задаче №17 нельзя использовать готовую формулу. Вам нужно написать математическую модель самостоятельно.

Научитесь хорошо считать в уме

Учитесь вычислять без калькулятора — некоторые задания требуют навыка быстрого счёта. К тому же, на экзамене вам нужно оставить как можно больше времени на сложные задачи и проверку.

Проверяйте решения и ответы

Например, убедитесь, что правильно перевели число из обычной дроби в десятичную. Арифметические ошибки также часто встречаются в задаче на финансовую математику

В задании №9 обратите внимание на знаки, особенно если вам попались тригонометрические функции

Также важно без ошибок определить ограничения x в задаче №13. Если исходное уравнение содержит tgx, то — cosx≠0

Если уравнение содержит квадратный корень, подкоренное выражение — ≥0

Если исходное уравнение содержит tgx, то — cosx≠0. Если уравнение содержит квадратный корень, подкоренное выражение — ≥0.

Проверяйте свои знания

Вы можете пройти тест на бесплатном вводном занятии с преподавателем или на сайте ФИПИ. Так вы узнаете, что помните хорошо, а что нужно повторить. Также вы можете воспользоваться нашей библиотекой знаний с полезными материалами для подготовки. Нужно только зарегистрироваться на сайте. 

Не бойтесь второй части 

Смело решайте задания из второй части. Попробуйте справиться с заданиями №13 и №15. Скорее всего, они вам хорошо знакомы. Чаще всего №13 оказывается не таким уж и сложным. Если вы хорошо знаете геометрию, начните с №14 или №16. Если вам по душе алгебра, решайте задачи на параметр и свойства чисел — №18, 19.

Отдыхайте 

Составьте комфортное расписание занятий. Подготовка к ЕГЭ по профильной математике в 2021 не должна быть тяжким бременем. Проводите больше времени на свежем воздухе, встречайтесь с друзьями и не забывайте про здоровый сон. 

Подготовка к экзамену по профильной математике

     На самом деле как бы ни напугали вас все нововведения и изменения, страх нужно откинуть в сторону. Впереди год плодотворной и усиленной работы, за который вы сможете совершить чудо. Хотя в вопросе экзаменов речь идет совсем не о волшебстве. 

     Прорабатывайте и нарешивайте задания по каждой теме, учите то, что за 11 лет школы далось не так хорошо, повторяйте материал, который знаете в совершенстве. Составьте личный план подготовки к ЕГЭ по профильной математике и не опускайте руки. Помните, что ЕГЭ как уравнение: поначалу мы видим много неизвестных, но в итоге находим решение! Удачи!

Следите за новостями о ЕГЭ по профильной математике 2022 вместе с Умскул. 

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Применение формул сокращенного умножения

1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.

$(a+b)^2=a^2+2ab+b^2$

2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

$(a-b)^2=a^2-2ab+b^2$

3. Разность квадратов раскладывается на произведение разности чисел и их сумму.

$a^2-b^2=(a+b)(a-b)$

4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.

$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.

$a^3+b^3=(a+b)(a^2-ab+b^2)$

7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.

$a^3-b^3=(a-b)(a^2+ab+b^2)$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Обратные тригонометрические функции и простейшие тригонометрические уравнения

Арккосинус

Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $$, косинус которого равен $а$.

Если, $|а|≤1$, то $arccos а = t ⇔ \{\table \cos (t)=a; \0≤t≤π;$

$arcos(-a) = π-arccos⁡a$, где $0≤а≤1$

Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение

$t=±arccos ⁡ a+2πk; k∈Z$

Частные случаи

$cos t =1, t = 2πk;k∈Z$

$cos t = 0, t = {π}/{2}+πk;k∈Z$

$cos t = -1, t=π+2πk;k∈Z$

Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$

$сos{2πx}/{3}=-{√3}/{2}$

${2πx}/{3}=±arccos⁡(-{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$

${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$

Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$

$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$

$x=±1,25+3k$

Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения

$k=0$

$x_1= -1,25$

$x_2=1,25$

$к=1$

$х_1=3-1,25=1,75$

$х_2=3+1,25=4,25$

Нам подходит $1,25$ – это и есть результат

Ответ: $1,25$

Арксинус

Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.

Если, $|а|≤1$, то $arcsin a = t ⇔ \{\table \sint=a; \-{π}/{2}≤t≤{π}/{2};$

$arcsin(-a)= — arcsin a$, где $0≤а≤1$

Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:

$1. t_1 = arcsin a+2πk;k∈Z$

$t_2 = (π- arcsin a)+ 2πk;k∈Z$

$2. t=(-1)^n arcsin ⁡ a+πn; n∈Z$

$3.$ Частные случаи

$sin t = 0, t=πk;k∈Z$

$sin t = 1, t={π}/{2}+2πk;k∈Z$

$sin t = -1,t=-{π}/{2}+2πk;k∈Z$

Арктангенс

$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.

$arctg a = t ⇔ \{\table \tgt=a; \-{π}/{2}≤t≤{π}/{2};$

$arctg(-a)= — arctg a$

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.

В ЕГЭ по математике базового уровня 6 тематических блоков:

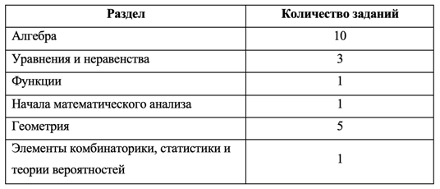
Тематические блоки, ЕГЭ по математике 2022, базовый уровень

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.

Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались

Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!

Что в итоге

Теперь вы знаете больше про ЕГЭ по математике 2022

Вы познакомились со структурой и поняли, на что стоит обращать внимание при подготовке. А еще узнали, что первую часть обязательно решать на максимум, а вторая не такая страшная, как кажется

Но наверняка у вас еще осталась куча вопросов: по оформлению и конкретному решению каких-то заданий точно.Обо всем этом я подробно рассказываю своим ученикам во время подготовки к ЕГЭ по математике. Мы изучаем все непонятные темы, а потом прорешиваем много однотипных заданий — так легче запоминается формат. Еще мы всегда проводим пробные экзамены, чтобы выявить слабые места. Я анализирую ошибки каждого ученика и индивидуально разбираю их с ними. Благодаря этому мои выпускники гарантированно сдают ЕГЭ на 80+. Если вы хотите оказаться среди них — записывайтесь на курсы!